Cross validation

Math 158 - Spring 2022

Jo Hardin (from Mine Çetinkaya-Rundel)

Agenda

• Cross validation for model evaluation
• Cross validation for model comparison

Data & goal

• Data: The data come from data.world, by way of TidyTuesday
• Goal: Compare two models which both predict imdb_rating from other variables in the dataset

office_ratings <- read_csv(here::here("slides", "data/office_ratings.csv"))
office_ratings

# A tibble: 188 × 6
   season episode title             imdb_rating total_votes air_date  
    <dbl>   <dbl> <chr>                   <dbl>       <dbl> <date>    
 1      1       1 Pilot                     7.6        3706 2005-03-24
 2      1       2 Diversity Day             8.3        3566 2005-03-29
 3      1       3 Health Care               7.9        2983 2005-04-05
 4      1       4 The Alliance              8.1        2886 2005-04-12
 5      1       5 Basketball                8.4        3179 2005-04-19
 6      1       6 Hot Girl                  7.8        2852 2005-04-26
 7      2       1 The Dundies               8.7        3213 2005-09-20
 8      2       2 Sexual Harassment         8.2        2736 2005-09-27
 9      2       3 Office Olympics           8.4        2742 2005-10-04
10      2       4 The Fire                  8.4        2713 2005-10-11
# … with 178 more rows

Modeling prep

Split data into training and testing

set.seed(123)
office_split <- initial_split(office_ratings)
office_train <- training(office_split)
office_test <- testing(office_split)

Specify model

office_spec <- linear_reg() %>%
  set_engine("lm")

office_spec

Linear Regression Model Specification (regression)

Computational engine: lm 

Model 1

Your roommate’s suggestion

• Create a recipe that uses the new variables we generated
• Denote episode as an ID variable and doesn’t use air_date as a predictor
• Consider season as a factor variable
• Create dummy variables for all nominal predictors
• Remove all zero variance predictors

Your thoughts

• Create a recipe that uses the new variables we generated
• Denote episode as an ID variable and doesn’t use air_date as a predictor
• Consider season as numeric
• Create dummy variables for all nominal predictors
• Remove all zero variance predictors

Create recipe 1

office_rec1 <- recipe(imdb_rating ~ ., data = office_train) %>%
  update_role(title, new_role = "id") %>%
  step_rm(air_date) %>%
  step_num2factor(season, levels = as.character(1:9)) %>%
  step_dummy(all_nominal_predictors()) %>%
  step_zv(all_predictors())

office_rec1

Data Recipe

Inputs:

      role #variables
        id          1
   outcome          1
 predictor          4

Operations:

Delete terms air_date
Factor variables from season
Dummy variables from all_nominal_predictors()
Zero variance filter on all_predictors()

Create recipe 2

season is now numeric

office_rec2 <- recipe(imdb_rating ~ ., data = office_train) %>%
  update_role(title, new_role = "id") %>%
  step_rm(air_date) %>%
  step_dummy(all_nominal_predictors()) %>%
  step_zv(all_predictors())

office_rec2

Data Recipe

Inputs:

      role #variables
        id          1
   outcome          1
 predictor          4

Operations:

Delete terms air_date
Dummy variables from all_nominal_predictors()
Zero variance filter on all_predictors()

Create workflow

office_wflow1 <- workflow() %>%
  add_model(office_spec) %>%
  add_recipe(office_rec1)

office_wflow1

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: linear_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
4 Recipe Steps

• step_rm()
• step_num2factor()
• step_dummy()
• step_zv()

── Model ───────────────────────────────────────────────────────────────────────
Linear Regression Model Specification (regression)

Computational engine: lm 

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: linear_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
3 Recipe Steps

• step_rm()
• step_dummy()
• step_zv()

── Model ───────────────────────────────────────────────────────────────────────
Linear Regression Model Specification (regression)

Computational engine: lm 

Fit model to training data

Actually, not so fast!

Cross validation

Spending our data

• We have already established that the idea of data spending where the test set was recommended for obtaining an unbiased estimate of performance.
• However, we need to decide which model to choose before using the test set.
• Typically we can’t decide on which final model to take to the test set without making model assessments.
• Remedy: Resampling to make model assessments on training data in a way that can generalize to new data.

Resampling for model assessment

Resampling is only conducted on the training set. The test set is not involved. For each iteration of resampling, the data are partitioned into two subsamples:

• The model is fit with the analysis set.
• The model is evaluated with the assessment set.

Resampling for model assessment

Source: Kuhn and Silge. Tidy modeling with R.

Analysis and assessment sets

• Analysis set is analogous to training set.
• Assessment set is analogous to test set.
• The terms analysis and assessment avoids confusion with initial split of the data.
• These data sets are mutually exclusive.

Cross validation

More specifically, v-fold cross validation – commonly used resampling technique:

• Randomly split your training data into v partitions
• Use 1 partition for assessment, and the remaining v-1 partitions for analysis
• Repeat v times, updating which partition is used for assessment each time

Let’s give an example where v = 3…

Cross validation, step 1

Randomly split your training data into 3 partitions:

Split data

set.seed(345)
folds <- vfold_cv(office_train, v = 3)
folds

#  3-fold cross-validation 
# A tibble: 3 × 2
  splits          id   
  <list>          <chr>
1 <split [94/47]> Fold1
2 <split [94/47]> Fold2
3 <split [94/47]> Fold3

Cross validation, steps 2 and 3

• Use 1 partition for assessment, and the remaining v-1 partitions for analysis
• Repeat v times, updating which partition is used for assessment each time

Fit resamples

set.seed(456)

office_fit_rs1 <- office_wflow1 %>%
  fit_resamples(folds)

office_fit_rs1

# Resampling results
# 3-fold cross-validation 
# A tibble: 3 × 4
  splits          id    .metrics         .notes          
  <list>          <chr> <list>           <list>          
1 <split [94/47]> Fold1 <tibble [2 × 4]> <tibble [0 × 1]>
2 <split [94/47]> Fold2 <tibble [2 × 4]> <tibble [0 × 1]>
3 <split [94/47]> Fold3 <tibble [2 × 4]> <tibble [0 × 1]>

set.seed(456)

office_fit_rs2 <- office_wflow2 %>%
  fit_resamples(folds)

office_fit_rs2

# Resampling results
# 3-fold cross-validation 
# A tibble: 3 × 4
  splits          id    .metrics         .notes          
  <list>          <chr> <list>           <list>          
1 <split [94/47]> Fold1 <tibble [2 × 4]> <tibble [0 × 1]>
2 <split [94/47]> Fold2 <tibble [2 × 4]> <tibble [0 × 1]>
3 <split [94/47]> Fold3 <tibble [2 × 4]> <tibble [0 × 1]>

Cross validation, now what?

• We’ve fit a bunch of models
• Now it’s time to use them to collect metrics (e.g., \(R^2\), RMSE) on each model and use them to evaluate model fit and how it varies across folds

Collect CV metrics

collect_metrics(office_fit_rs1)

# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 rmse    standard   0.373     3  0.0324 Preprocessor1_Model1
2 rsq     standard   0.574     3  0.0614 Preprocessor1_Model1

collect_metrics(office_fit_rs2)

# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 rmse    standard   0.407     3 0.00971 Preprocessor1_Model1
2 rsq     standard   0.438     3 0.0857  Preprocessor1_Model1

Choose Model 1.

Deeper look into CV metrics

cv_metrics1 <- collect_metrics(office_fit_rs1, summarize = FALSE) 

cv_metrics1

# A tibble: 6 × 5
  id    .metric .estimator .estimate .config             
  <chr> <chr>   <chr>          <dbl> <chr>               
1 Fold1 rmse    standard       0.320 Preprocessor1_Model1
2 Fold1 rsq     standard       0.687 Preprocessor1_Model1
3 Fold2 rmse    standard       0.368 Preprocessor1_Model1
4 Fold2 rsq     standard       0.476 Preprocessor1_Model1
5 Fold3 rmse    standard       0.432 Preprocessor1_Model1
6 Fold3 rsq     standard       0.558 Preprocessor1_Model1

Better tabulation of CV metrics

cv_metrics1 %>%
  mutate(.estimate = round(.estimate, 3)) %>%
  pivot_wider(id_cols = id, names_from = .metric, values_from = .estimate) %>%
  kable(col.names = c("Fold", "RMSE", "R-squared"))

Fold	RMSE	R-squared
Fold1	0.320	0.687
Fold2	0.368	0.476
Fold3	0.432	0.558

How does RMSE compare to y?

Cross validation RMSE stats:

cv_metrics1 %>%
  filter(.metric == "rmse") %>%
  summarise(
    min = min(.estimate),
    max = max(.estimate),
    mean = mean(.estimate),
    sd = sd(.estimate)
  )

# A tibble: 1 × 4
    min   max  mean     sd
  <dbl> <dbl> <dbl>  <dbl>
1 0.320 0.432 0.373 0.0562

Training data IMDB score stats:

office_ratings %>%
  summarise(
    min = min(imdb_rating),
    max = max(imdb_rating),
    mean = mean(imdb_rating),
    sd = sd(imdb_rating)
  )

# A tibble: 1 × 4
    min   max  mean    sd
  <dbl> <dbl> <dbl> <dbl>
1   6.7   9.7  8.26 0.538

Cross validation jargon

• Referred to as v-fold or k-fold cross validation
• Also commonly abbreviated as CV

Cross validation, for reals

• To illustrate how CV works, we used v = 3:

  • Analysis sets are 2/3 of the training set
  • Each assessment set is a distinct 1/3
  • The final resampling estimate of performance averages each of the 3 replicates

• This was useful for illustrative purposes, but v = 3 is a poor choice in practice

• Values of v are most often 5 or 10; we generally prefer 10-fold cross-validation as a default

Bias-Variance tradeoff

\[\begin{align} \mbox{prediction error } = \mbox{ irreducible error } + \mbox{ bias } + \mbox{ variance} \end{align}\]

• irreducible error is the natural variability that comes with observations.

• bias of the model represents the difference between the true model and a model which is too simple. The more complicated the model, the closer the points are to the prediction.

• variance represents the variability of the model from sample to sample. A simple model would not change a lot from sample to sample.

Bias-Variance tradeoff

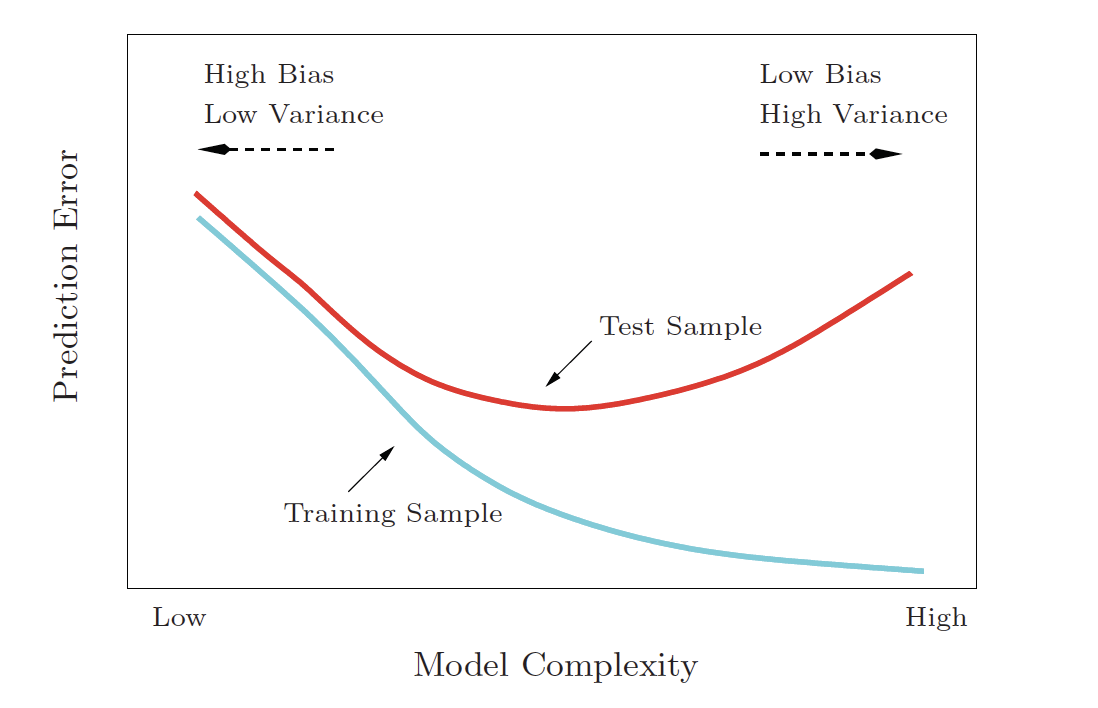
Credit: An Introduction to Statistical Learning, James et al.